Множество значений функции примеры и решения. Решение типовых задач

Зачастую в рамках решения задач нам приходится искать множество значений функции на области определения или отрезке. Например, это нужно делать при решении разных типов неравенств, оценках выражений и др.

В рамках этого материала мы расскажем, что из себя представляет область значений функции, приведем основные методы, которыми ее можно вычислить, и разберем задачи различной степени сложности. Для наглядности отдельные положения проиллюстрированы графиками. Прочитав эту статью, вы получите исчерпывающее представление об области значений функции.

Начнем с базовых определений.

Определение 1

Множество значений функции y = f (x) на некотором интервале x представляет собой множество всех значений, которые данная функция принимает при переборе всех значений x ∈ X .

Определение 2

Область значений функции y = f (x) – это множество всех ее значений, которые она может принять при переборе значений x из области x ∈ (f) .

Область значений некоторой функции принято обозначать E (f) .

Обратите внимание, что понятие множества значений функции не всегда тождественно области ее значений. Эти понятия будут равнозначны только в том случае, если интервал значений x при нахождении множества значений совпадет с областью определения функции.

Важно также различать область значений и область допустимых значений переменной x для выражения в правой части y = f (x) . Область допустимых значений x для выражения f (x) и будет областью определения данной функции.

Ниже приводится иллюстрация, на которой показаны некоторые примеры. Синие линии – это графики функций, красные – асимптоты, рыжие точки и линии на оси ординат – это области значений функции.

Очевидно, что область значений функции можно получить при проецировании графика функции на ось O y . При этом она может представлять собой как одно число, так и множество чисел, отрезок, интервал, открытый луч, объединение числовых промежутков и др.

Рассмотрим основные способы нахождения области значений функции.

Начнем с определения множества значений непрерывной функции y = f (x) на некотором отрезке, обозначенном [ a ; b ] . Мы знаем, что функция, непрерывная на некотором отрезке, достигает на нем своего минимума и максимума, то есть наибольшего m a x x ∈ a ; b f (x) и наименьшего значения m i n x ∈ a ; b f (x) . Значит, у нас получится отрезок m i n x ∈ a ; b f (x) ; m a x x ∈ a ; b f (x) , в котором и будут находиться множества значений исходной функции. Тогда все, что нам нужно сделать, – это найти на этом отрезке указанные точки минимума и максимума.

Возьмем задачу, в которой нужно определить область значений арксинуса.

Пример 1

Условие: найдите область значений y = a r c sin x .

Решение

В общем случае область определения арксинуса располагается на отрезке [ - 1 ; 1 ] . Нам надо определить наибольшее и наименьшее значение указанной функции на нем.

y " = a r c sin x " = 1 1 - x 2

Мы знаем, что производная функции будет положительной для всех значений x , расположенных в интервале [ - 1 ; 1 ] , то есть на протяжении всей области определения функция арксинуса будет возрастать. Значит, самое маленькое значение она примет при x , равном - 1 , а самое большое – при x , равном 1 .

m i n x ∈ - 1 ; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2

Таким образом, область значений функции арксинус будет равна E (a r c sin x) = - π 2 ; π 2 .

Ответ: E (a r c sin x) = - π 2 ; π 2

Пример 2

Условие: вычислите область значений y = x 4 - 5 x 3 + 6 x 2 на заданном отрезке [ 1 ; 4 ] .

Решение

Все, что нам нужно сделать, – это вычислить наибольшее и наименьшее значение функции в заданном интервале.

Для определения точек экстремума надо произвести следующие вычисления:

y " = x 4 - 5 x 3 + 6 x 2 " = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12) = 0 x 1 = 0 ∉ 1 ; 4 и л и 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 · 4 · 12 = 33 x 2 = 15 - 33 8 ≈ 1 . 16 ∈ 1 ; 4 ; x 3 = 15 + 33 8 ≈ 2 . 59 ∈ 1 ; 4

Теперь найдем значения заданной функции в концах отрезка и точках x 2 = 15 - 33 8 ; x 3 = 15 + 33 8:

y (1) = 1 4 - 5 · 1 3 + 6 · 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 · 15 - 33 8 3 + 6 · 15 - 33 8 2 = = 117 + 165 33 512 ≈ 2 . 08 y 15 + 33 8 = 15 + 33 8 4 - 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 y (4) = 4 4 - 5 · 4 3 + 6 · 4 2 = 32

Значит, множество значений функции будет определяться отрезком 117 - 165 33 512 ; 32 .

Ответ: 117 - 165 33 512 ; 32 .

Перейдем к нахождению множества значений непрерывной функции y = f (x) в промежутках (a ; b) , причем a ; + ∞ , - ∞ ; b , - ∞ ; + ∞ .

Начнем с определения наибольшей и наименьшей точки, а также промежутков возрастания и убывания на заданном интервале. После этого нам нужно будет вычислить односторонние пределы в концах интервала и/или пределы на бесконечности. Иными словами, нам надо определить поведении функции в заданных условиях. Для этого у нас есть все необходимые данные.

Пример 3

Условие: вычислите область значений функции y = 1 x 2 - 4 на интервале (- 2 ; 2) .

Решение

Определяем наибольшее и наименьшее значение функции на заданном отрезке

y " = 1 x 2 - 4 " = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2 ; 2)

У нас получилось максимальное значение, равное 0 , поскольку именно в этой точке происходит перемена знака функции и график переходит к убыванию. См. на иллюстрацию:

То есть y (0) = 1 0 2 - 4 = - 1 4 будет максимальным значений функции.

Теперь определим поведение функции при таком x, который стремится к - 2 с правой стороны и к + 2 с левой стороны. Иными словами, найдем односторонние пределы:

lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 · 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 · 1 - 0 = - ∞

У нас получилось, что значения функции будут возрастать от минус бесконечности до - 1 4 тогда, когда аргумент изменяется в пределах от - 2 до 0 . А когда аргумент меняется от 0 до 2 , значения функции убывают к минус бесконечности. Следовательно, множеством значений заданной функции на нужном нам интервале будет (- ∞ ; - 1 4 ] .

Ответ: (- ∞ ; - 1 4 ] .

Пример 4

Условие : укажите множество значений y = t g x на заданном интервале - π 2 ; π 2 .

Решение

Нам известно, что в общем случае производная тангенса в - π 2 ; π 2 будет положительной, то есть функция будет возрастать. Теперь определим, как ведет себя функция в заданных границах:

lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞

Мы получили рост значений функции от минус бесконечности к плюс бесконечности при изменении аргумента от - π 2 до π 2 ,и можно сказать, что множеством решений данной функции будет множество всех действительных чисел.

Ответ: - ∞ ; + ∞ .

Пример 5

Условие: определите, какова область значений функции натурального логарифма y = ln x .

Решение

Нам известно, что данная функция является определенной при положительных значениях аргумента D (y) = 0 ; + ∞ . Производная на заданном интервале будет положительной: y " = ln x " = 1 x . Значит, на нем происходит возрастание функции. Далее нам нужно определить односторонний предел для того случая, когда аргумент стремится к 0 (в правой части), и когда x стремится к бесконечности:

lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞

Мы получили, что значения функции будут возрастать от минус бесконечности до плюс бесконечности при изменении значений x от нуля до плюс бесконечности. Значит, множество всех действительных чисел – это и есть область значений функции натурального логарифма.

Ответ: множество всех действительных чисел – область значений функции натурального логарифма.

Пример 6

Условие: определите, какова область значений функции y = 9 x 2 + 1 .

Решение

Данная функция является определенной при условии, что x – действительное число. Вычислим наибольшие и наименьшие значения функции, а также промежутки ее возрастания и убывания:

y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0

В итоге мы определили, что данная функция будет убывать, если x ≥ 0 ; возрастать, если x ≤ 0 ; она имеет точку максимума y (0) = 9 0 2 + 1 = 9 при переменной, равной 0 .

Посмотрим, как же ведет себя функция на бесконечности:

lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 · 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 · 1 + ∞ = + 0

Из записи видно, что значения функции в этом случае будут асимптотически приближаться к 0.

Подведем итоги: когда аргумент изменяется от минус бесконечности до нуля, то значения функции возрастают от 0 до 9 . Когда значения аргумента меняются от 0 до плюс бесконечности, соответствующие значения функции будут убывать от 9 до 0 . Мы отобразили это на рисунке:

На нем видно, что областью значений функции будет интервал E (y) = (0 ; 9 ]

Ответ: E (y) = (0 ; 9 ]

Если нам надо определить множество значений функции y = f (x) на промежутках [ a ; b) , (a ; b ] , [ a ; + ∞) , (- ∞ ; b ] , то нам понадобится провести точно такие же исследования. Эти случаи мы пока не будем разбирать: далее они нам еще встретятся в задачах.

А как быть в случае, если область определения некоторой функции представляет из себя объединение нескольких промежутков? Тогда нам надо вычислить множества значений на каждом из этих промежутков и объединить их.

Пример 7

Условие: определите, какова будет область значений y = x x - 2 .

Решение

Поскольку знаменатель функции не должен быть обращен в 0 , то D (y) = - ∞ ; 2 ∪ 2 ; + ∞ .

Начнем с определения множества значений функции на первом отрезке - ∞ ; 2 , который представляет из себя открытый луч. Мы знаем, что функция на нем будет убывать, то есть производная данной функции будет отрицательной.

lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0

Тогда в тех случаях, когда аргумент изменяется по направлению к минус бесконечности, значения функции будут асимптотически приближаться к 1 . Если же значения x меняются от минус бесконечности до 2 , то значения будут убывать от 1 до минус бесконечности, т.е. функция на этом отрезке примет значения из интервала - ∞ ; 1 . Единицу мы исключаем из наших рассуждений, поскольку значения функции ее не достигают, а лишь асимптотически приближаются к ней.

Для открытого луча 2 ; + ∞ производим точно такие же действия. Функция на нем также является убывающей:

lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0

Значения функции на данном отрезке определяются множеством 1 ; + ∞ . Значит, нужная нам область значений функции, заданной в условии, будет объединением множеств - ∞ ; 1 и 1 ; + ∞ .

Ответ: E (y) = - ∞ ; 1 ∪ 1 ; + ∞ .

Это можно увидеть на графике:

Особый случай – периодические функции. Их область значения совпадает с множеством значений на том промежутке, который отвечает периоду этой функции.

Пример 8

Условие: определите область значений синуса y = sin x .

Решение

Синус относится к периодической функции, а его период составляет 2 пи. Берем отрезок 0 ; 2 π и смотрим, каким будет множество значений на нем.

y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z

В рамках 0 ; 2 π у функции будут точки экстремума π 2 и x = 3 π 2 . Подсчитаем, чему будут равны значения функции в них, а также на границах отрезка, после чего выберем самое большое и самое маленькое значение.

y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1 , max x ∈ 0 ; 2 π sin x = sin π 2 = 1

Ответ: E (sin x) = - 1 ; 1 .

Если вам нужно знать области значений таких функций, как степенная, показательная, логарифмическая, тригонометрическая, обратная тригонометрическая, то советуем вам перечитать статью об основных элементарных функциях. Теория, которую мы приводим здесь, позволяет проверить указанные там значения. Их желательно выучить, поскольку они часто требуются при решении задач. Если вы знаете области значений основных функций, то легко сможете находить области функций, которые получены из элементарных с помощью геометрического преобразования.

Пример 9

Условие: определите область значения y = 3 a r c cos x 3 + 5 π 7 - 4 .

Решение

Нам известно, что отрезок от 0 до пи есть область значений арккосинуса. Иными словами, E (a r c cos x) = 0 ; π или 0 ≤ a r c cos x ≤ π . Мы можем получить функцию a r c cos x 3 + 5 π 7 из арккосинуса, сдвинув и растянув ее вдоль оси O x , но такие преобразования нам ничего не дадут. Значит, 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .

Функция 3 a r c cos x 3 + 5 π 7 может быть получена из арккосинуса a r c cos x 3 + 5 π 7 с помощью растяжения вдоль оси ординат, т.е. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Финалом преобразований является сдвиг вдоль оси O y на 4 значения. В итоге получаем двойное неравенство:

0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4

Мы получили, что нужная нам область значений будет равна E (y) = - 4 ; 3 π - 4 .

Ответ: E (y) = - 4 ; 3 π - 4 .

Еще один пример запишем без пояснений, т.к. он полностью аналогичен предыдущему.

Пример 10

Условие: вычислите, какова будет область значений функции y = 2 2 x - 1 + 3 .

Решение

Перепишем функцию, заданную в условии, как y = 2 · (2 x - 1) - 1 2 + 3 . Для степенной функции y = x - 1 2 область значений будет определена на промежутке 0 ; + ∞ , т.е. x - 1 2 > 0 . В таком случае:

2 x - 1 - 1 2 > 0 ⇒ 2 · (2 x - 1) - 1 2 > 0 ⇒ 2 · (2 x - 1) - 1 2 + 3 > 3

Значит, E (y) = 3 ; + ∞ .

Ответ: E (y) = 3 ; + ∞ .

Теперь разберем, как найти область значений функции, которая не является непрерывной. Для этого нам надо разбить всю область на промежутки и найти множества значений на каждом из них, после чего объединить то, что получилось. Чтобы лучше понять это, советуем повторить основные виды точек разрыва функции.

Пример 11

Условие: дана функция y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3 < x ≤ 3 1 x - 3 , x > 3 . Вычислите область ее значений.

Решение

Данная функция является определенной для всех значений x . Проведем ее анализ на непрерывность при значениях аргумента, равных - 3 и 3:

lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)

Имеем неустранимый разрыв первого рода при значении аргумента - 3 . При приближении к нему значения функции стремятся к - 2 sin 3 2 - 4 , а при стремлении x к - 3 с правой стороны значения будут стремиться к - 1 .

lim x → 3 - 0 f (x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f (x) = lim x → 3 + 0 1 x - 3 = + ∞

Имеем неустранимый разрыв второго рода в точке 3 . Когда функция стремится к нему, ее значения приближаются к - 1 , при стремлении к той же точке справа – к минус бесконечности.

Значит, вся область определения данной функции является разбитой на 3 интервала (- ∞ ; - 3 ] , (- 3 ; 3 ] , (3 ; + ∞) .

На первом из них у нас получилась функция y = 2 sin x 2 - 4 . Поскольку - 1 ≤ sin x ≤ 1 , получаем:

1 ≤ sin x 2 < 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2

Значит, на данном промежутке (- ∞ ; - 3 ] множество значении функции – [ - 6 ; 2 ] .

На полуинтервале (- 3 ; 3 ] получилась постоянная функция y = - 1 . Следовательно, все множество ее значений в данном случае будет сводится к одному числу - 1 .

На втором промежутке 3 ; + ∞ у нас есть функция y = 1 x - 3 . Она является убывающей, потому что y " = - 1 (x - 3) 2 < 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:

lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0

Значит, множество значений исходной функции при x > 3 представляет собой множество 0 ; + ∞ . Теперь объединим полученные результаты: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; + ∞ .

Ответ: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; + ∞ .

Решение показано на графике:

Пример 12

Условие: есть функция y = x 2 - 3 e x . Определите множество ее значений.

Решение

Она определена для всех значений аргумента, представляющих собой действительные числа. Определим, в каких промежутках данная функция будет возрастать, а в каких убывать:

y " = x 2 - 3 e x " = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x

Мы знаем, что производная обратится в 0 , если x = - 1 и x = 3 . Поместим эти две точки на ось и выясним, какие знаки будет иметь производная на получившихся интервалах.

Функция будет убывать на (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) и возрастать на [ - 1 ; 3 ] . Точкой минимума будет - 1 , максимума – 3 .

Теперь найдем соответствующие значения функции:

y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3

Посмотрим на поведение функции на бесконечности:

lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 " e x " = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x " (e x) " = 2 lim x → + ∞ 1 e x = 2 · 1 + ∞ = + 0

Для вычисления второго предела было использовано правило Лопиталя. Изобразим ход нашего решения на графике.

На нем видно, что значения функции будут убывать от плюс бесконечности до - 2 e тогда, когда аргумент меняется от минус бесконечности до - 1 . Если же он изменяется от 3 до плюс бесконечности, то значения будут убывать от 6 e - 3 до 0 , но при этом 0 достигнут не будет.

Таким образом, E (y) = [ - 2 e ; + ∞) .

Ответ: E (y) = [ - 2 e ; + ∞)

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Сегодня на уроке мы обратимся к одному из основных понятий математики - понятию функции; более детально рассмотрим одно из свойств функции - множество ее значений.

Ход урока

Учитель. Решая задачи, мы замечаем, что подчас именно нахождение множества значений функции ставит нас в затруднительные ситуации. Почему? Казалось бы, изучая функцию с 7-го класса, мы знаем о ней достаточно много. Поэтому у нас есть все основания сделать упреждающий ход. Давайте сегодня сами «поиграем» с множеством значений функции, чтобы снять многие вопросы этой темы на предстоящем экзамене.

Множества значений элементарных функций

Учитель. Для начала необходимо повторить графики, уравнения и множества значений основных элементарных функций на всей области определения.

На экран проецируются графики функций: линейной, квадратичной, дробно-рациональной, тригонометрических, показательной и логарифмической, для каждой из них устно определяется множество значений. Обратите внимание учащихся на то, что у линейной функции E(f) = R или одно число, у дробно-линейной

Это наша азбука. Присоединив к ней наши знания о преобразованиях графиков: параллельный перенос, растяжение, сжатие, отражение, мы сможем решить задачи первой части ЕГЭ и даже чуть сложнее. Проверим это.

Самостоятельная работа

Условия задач и системы координат напечатаны для каждого ученика .

1. Найдите множество значений функции на всей области определения:

а) y = 3 sin х ;
б) y = 7 – 2 х ;
в) y = –arccos (x + 5):
г) y = | arctg x |;
д)

2. Найдите множество значений функции y = x 2 на промежутке J , если:

а) J = ;
б) J = [–1; 5).

3. Задайте функцию аналитически (уравнением), если множество ее значений:

1) E (f (x )) = (–∞ ; 2] и f (x ) - функция

а) квадратичная,
б) логарифмическая,
в) показательная;

2) E (f (x )) = R \{7}.

При обсуждении задания 2 самостоятельной работы обратите внимание учащихся на то, что, в случае монотонности и непрерывности функции y = f (x ) на заданном промежутке [a ; b ], множество ее значений - промежуток , концами которого являются значения f (a ) и f (b ).

Варианты ответов к заданию 3.

1.
а) y = –x 2 + 2 , y = –(x + 18) 2 + 2,
y = a (x – x в) 2 + 2 при а < 0.

б) y = –| log 8 x | + 2,

в) y = –| 3 x – 7 | + 2, y = –5 | x | + 3.

2.
а) б)

в) y = 12 – 5x , где x ≠ 1 .

Нахождение множества значений функции с помощью производной

Учитель. В 10-м классе мы знакомились с алгоритмом нахождения экстремумов непрерывной на отрезке функции и отыскания ее множества значений, не опираясь на график функции. Вспомните, как мы это делали? (С помощью производной .) Давайте вспомним этот алгоритм.

Задачи на применение данного алгоритма встречаются в вариантах ЕГЭ. Так, например, в 2008 году была предложена такая задача. Вам предстоит решить ее дома .

Задание С1. Найдите наибольшее значение функции

f (x ) = (0,5x + 1) 4 – 50(0,5x + 1) 2

при | x + 1| ≤ 3.

Условия домашних задач распечатаны для каждого ученика .

Нахождение множества значений сложной функции

Учитель. Основную часть нашего урока составят нестандартные задачи, содержащие сложные функции, производные от которых являются очень сложными выражениями. Да и графики этих функций нам неизвестны. Поэтому для решения мы будем использовать определение сложной функции, то есть зависимость между переменными в порядке их вложенности в данную функцию, и оценку их области значений (промежутка изменения их значений). Задачи такого вида встречаются во второй части ЕГЭ. Обратимся к примерам.

Задание 1. Для функций y = f (x ) и y = g (x ) записать сложную функцию y = f (g (x )) и найти ее множество значений:

а) f (x ) = –x 2 + 2x + 3, g (x ) = sin x ;
б) f (x ) = –x 2 + 2x + 3, g (x ) = log 7 x ;
в) g (x ) = x 2 + 1;
г)

Решение. а) Сложная функция имеет вид: y = –sin 2 x + 2sin x + 3.

Вводя промежуточный аргумент t , мы можем записать эту функцию так:

y = –t 2 + 2t + 3, где t = sin x .

У внутренней функции t = sin x аргумент принимает любые значения, а множество ее значений - отрезок [–1; 1].

Таким образом, для внешней функции y = –t 2 +2t + 3 мы узнали промежуток изменения значений ее аргумента t : t [–1; 1]. Обратимся к графику функции y = –t 2 +2t + 3.

Замечаем, что квадратичная функция при t [–1; 1] принимает наименьшее и наибольшее значения на его концах: y наим = y (–1) = 0 и y наиб = y (1) = 4. А так как эта функция непрерывна на отрезке [–1; 1], то она принимает и все значения между ними.

Ответ : y .

б) Композиция этих функций приводит нас к сложной функции которая после введения промежуточного аргумента, может быть представлена так:

y = –t 2 + 2t + 3, где t = log 7 x ,

У функции t = log 7 x

x (0; +∞ ), t (–∞ ; +∞ ).

У функции y = –t 2 + 2t + 3 (см. график) аргумент t принимает любые значения, а сама квадратичная функция принимает все значения не больше 4.

Ответ : y (–∞ ; 4].

в) Сложная функция имеет следующий вид:

Вводя промежуточный аргумент, получаем:

где t = x 2 + 1.

Так как для внутренней функции x R , а t .

Ответ : y (0; 3].

г) Композиция двух данных функций дает нам сложную функцию

которая может быть записана как

Заметим, что

Значит, при

где k Z , t [–1; 0) (0; 1].

Нарисовав график функции видим, что при этих значениях t

y (–∞ ; –4] c ;

б) на всей области определения.

Решение. Вначале исследуем данную функцию на монотонность. Функция t = arcctg x - непрерывная и убывающая на R и множество ее значений (0; π). Функция y = log 5 t определена на промежутке (0; π), непрерывна и возрастает на нем. Значит, данная сложная функция убывает на множестве R . И она, как композиция двух непрерывных функций, будет непрерывна на R .

Решим задачу «а».

Так как функция непрерывна на всей числовой оси, то она непрерывна и на любой ее части, в частности, на данном отрезке. А тогда она на этом отрезке имеет наименьшее и наибольшее значения и принимает все значения между ними:

f

Какое из полученных значений больше? Почему? И каким же будет множество значений?

Ответ:

Решим задачу «б».

Ответ: у (–∞ ; log 5 π) на всей области определения.

Задача с параметром

Теперь попробуем составить и решить несложное уравнение с параметром вида f (x ) = a , где f (x ) - та же функция, что и в задании 4.

Задание 5. Определите количество корней уравнения log 5 (arcctg x ) = а для каждого значения параметра а .

Решение. Как мы уже показали в задании 4, функция у = log 5 (arcctg x ) - убывает и непрерывна на R и принимает значения меньше log 5 π. Этих сведений достаточно, чтобы дать ответ.

Ответ: если а < log 5 π, то уравнение имеет единственный корень;

если а ≥ log 5 π, то корней нет.

Учитель. Сегодня мы рассмотрели задачи, связанные с нахождением множества значений функции. На этом пути мы открыли для себя новый метод решения уравнений и неравенств - метод оценки, поэтому нахождение множества значений функции стало средством решения задач более высокого уровня. При этом мы увидели, как конструируются такие задачи и как свойства монотонности функции облегчают их решение.

И мне хочется надеяться, что та логика, которая связала рассмотренные сегодня задачи, вас поразила или хотя бы удивила. Иначе и быть не может: восхождение на новую вершину никого не оставляет равнодушным! Мы замечаем и ценим красивые картины, скульптуры и т.д. Но и в математике есть своя красота, притягивающая и завораживающая - красота логики. Математики говорят, что красивое решение - это, как правило, правильное решение, и это не просто фраза. Теперь Вам самим предстоит находить такие решения и один из путей к ним мы указали сегодня. Удачи вам! И помните: дорогу осилит идущий!

Зависимость одной переменной от другой называется функциональной зависимостью. Зависимость переменной y от переменной x называется функцией , если каждому значению x соответствует единственное значение y .

Обозначение:

Переменную x называют независимой переменной или аргументом , а переменную y - зависимой. Говорят, что y является функцией от x . Значение y , соответствующее заданному значению x , называют значением функции .

Все значения, которые принимает x , образуют область определения функции ; все значения, которые принимает y , образуют множество значений функции .

Обозначения:

D(f) - значения аргумента. E(f) - значения функции. Если функция задана формулой, то считают, что область определения состоит из всех значений переменной, при которых эта формула имеет смысл.

Графиком функции называется множество всех точек на координатной плоскости , абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции. Если некоторому значению x=x 0 соответствуют несколько значений (а не одно) y , то такое соответствие не является функцией. Для того чтобы множество точек координатной плоскости являлось графиком некоторой функции, необходимо и достаточно, чтобы любая прямая параллельная оси Оу, пересекалась с графиком не более чем в одной точке.

Способы задания функции

1) Функция может быть задана аналитически в виде формулы. Например,

2) Функция может быть задана таблицей из множества пар (x; y) .

3) Функция может быть задана графически. Пары значений (x; y) изображаются на координатной плоскости.

Монотонность функции

Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы "взбираться" вверх по графику.

Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции. Представьте, что некоторая точка движется по графику слева направо. Тогда точка будет как бы "скатываться" вниз по графику.

Функция, только возрастающая или только убывающая на данном числовом промежутке, называется монотонной на этом промежутке.

Нули функции и промежутки знакопостоянства

Значения х , при которых y=0 , называется нулями функции . Это абсциссы точек пересечения графика функции с осью Ох.

Такие промежутки значений x , на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.

Четные и нечетные функции

Четная функция
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.

Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x , принадлежащего области определения, выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).

Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.

Периодические функции

Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T) . T - это период функции.

Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.

Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.

Функция-это модель. Определим X, как множество значений независимой переменной // независимая -значит любая.

Функция это правило, с помощью которого по каждому значению независимой переменной из множества X можно найти единственное значение зависимой переменной. // т.е. для каждого х есть один у.

Из определения следует, что существует два понятия- независимая переменная (которую обозначаем х и она может принимать любые значения) и зависимая переменная (которую обозначаем y или f(х) и она высчитывается из функции, когда мы подставляем х).

НАПРИМЕР у=5+х

1. Независимая -это х, значит берем любое значение, пусть х=3

2. а теперь вычисляем у, значит у=5+х=5+3=8. (у зависима от х, потому что какой х подставим, такой у и получим)

Говорят, что переменная y функционально зависит от переменной x и обозначается это следующим образом: y = f (x).

НАПРИМЕР.

1.у=1/х. (наз.гипербола)

2. у=х^2. (наз. парабола)

3.у=3х+7. (наз. прямая)

4. у= √ х. (наз. ветвь параболы)

Независимая переменная (кот. мы обозначаем х) имеет название аргумент функции.

Область определения функции

Множество всех значений, которые принимает аргумент функции, называется областью определения функции и обозначается D (f) или D (y).

Рассмотрим D (у) для 1.,2.,3.,4.

1. D (у)= (∞; 0) и (0;+∞) //всё множество действительных чисел, кроме нуля.

2. D (у)= (∞; +∞)//всё мн-во действит.чисел

3. D (у)= (∞; +∞)//всё мн-во действит.чисел

4. D (у)= .

1) у = cos 2х 2) у = sin 2 x 3) y = cos 2 x +2

4) y = 2 sin 4 x

6. Найдите множество значений функции y = tg 2 x на отрезке

7. Найдите сумму всех целых чисел, которые входят в область значений функции y = 4 cos 2 x – 7.

1) -25 2) 25 3) -22 4) 0

Вариант 2

y = 2 cos 5 x +3.

1) (2;3) 2) 3) (1;5) 4) .

2. Найдите область значения функции

1) 3) (-∞;∞) 4) .

3. Укажите наименьшее число из области значений функции

1) 4 2) -3 3) 1 4) -7

4. Укажите наибольшее целое из области значений функции

1) 2 2) 13 3) 12 4) -2

5. Укажите функцию, множеством значений которой является отрезок [-5;5].

1) y = sin 5x 2) y = 5 cos 5x 3) y = cos (-5x)

4) y = sin 5x + 5

6. Найдите множество значений функции
на отрезке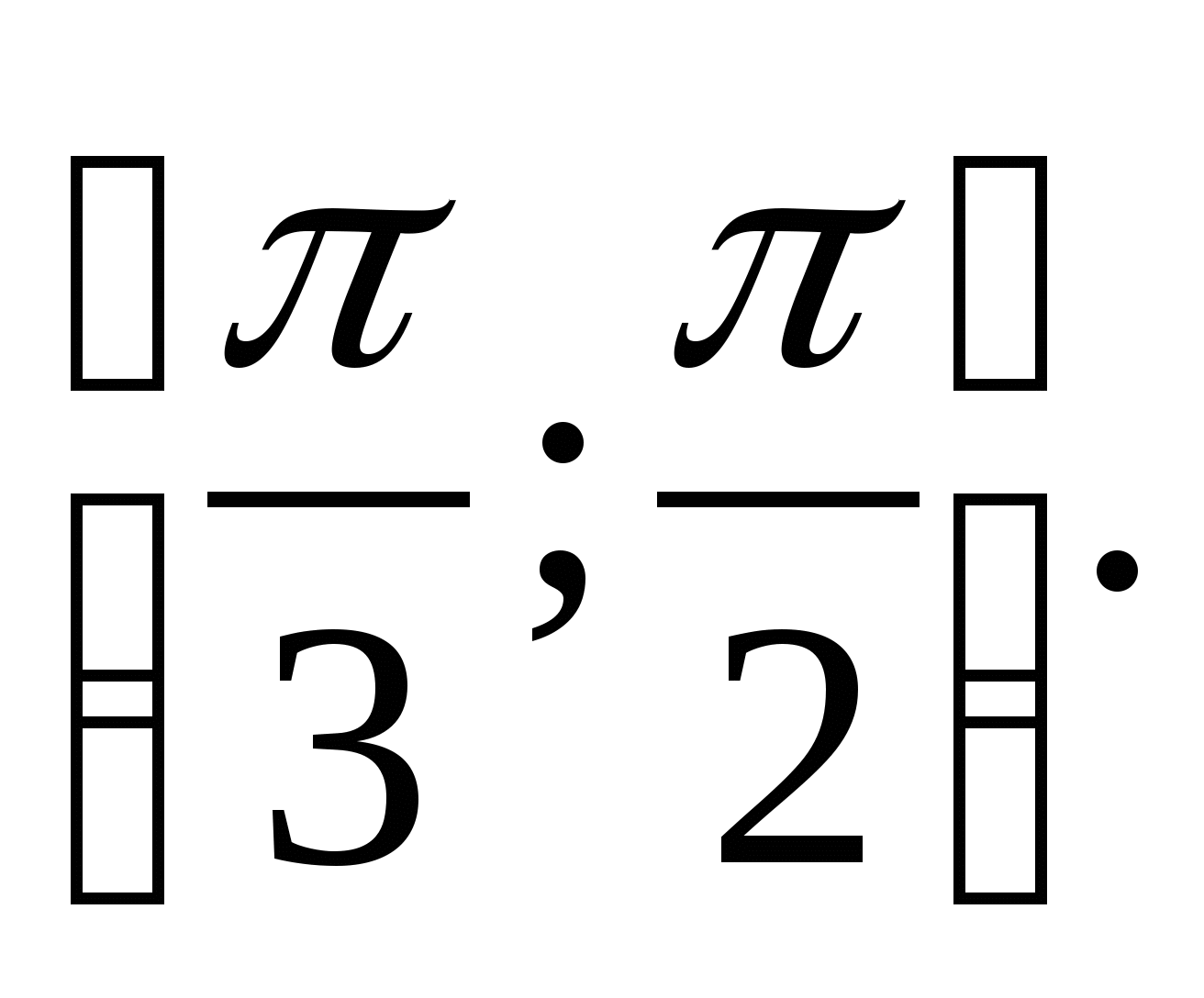

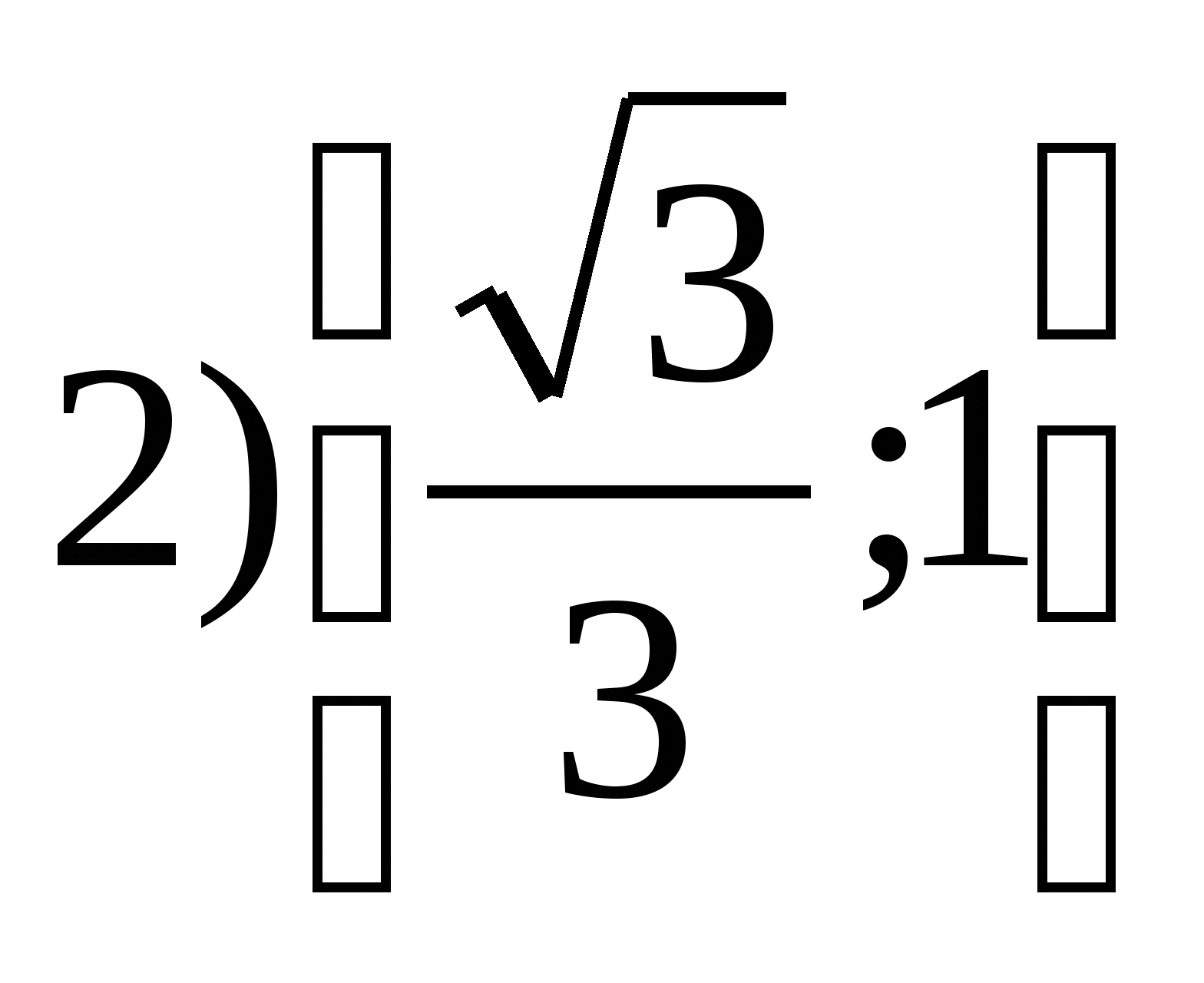
7. Найдите произведение всех целых чисел, которые входят в область значений функции у = 5 – 3 sin 2 x .

1) 120 2) 14 3) -15 4) 0

Вариант 3
1. Укажите множество значений функции y = sin 3 x + 5.

1) (-4;6) 2) 3) [-1;5) 4) (0;6)

1) 2) (0;3) 3) (1;3) 4) [-1;3)

3. Укажите наименьшее число из области значений функции у = 5 tg 2 x +2?

1) 5 2) 0 3) 7 4) 2

1) -1 2) -2,7 3) -2,3 4)-3

5. Укажите функцию, множеством значений которой является отрезок

[-17;-13].

1) y = 5 sin x – 8 3) y = -cos x +15

2) y = 2 cos x – 15 4) y = 3 sin x +10

6. Укажите наименьшее натуральное число, которое не входит в множество значений функции

1) 2 2) 4 3) 15 4) 6

7. Сколько целых чисел принадлежит множеству значений функции

y = 2 cos 3 x +10?

1) 2 2) 3 3) 4 5) 5

Вариант 4

1) 2) 4) (-7;-6)

2. Найдите область значений функции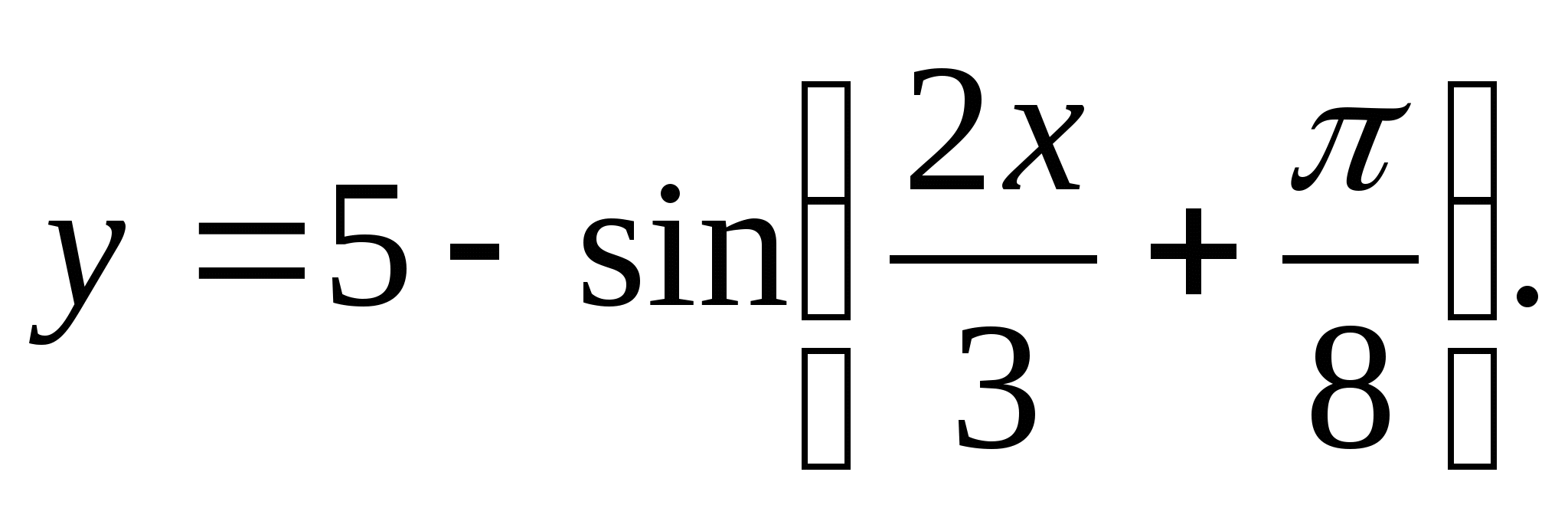

1) (1;5) 2) 3) (4;6) 4) [-6;-4]

3. Укажите наибольшее число из области значений функции y = -3 ctg 2 x +7.

1) 10 2) 4 3) 7 4) -3

4. Какое из следующих чисел не входит в множество значений функции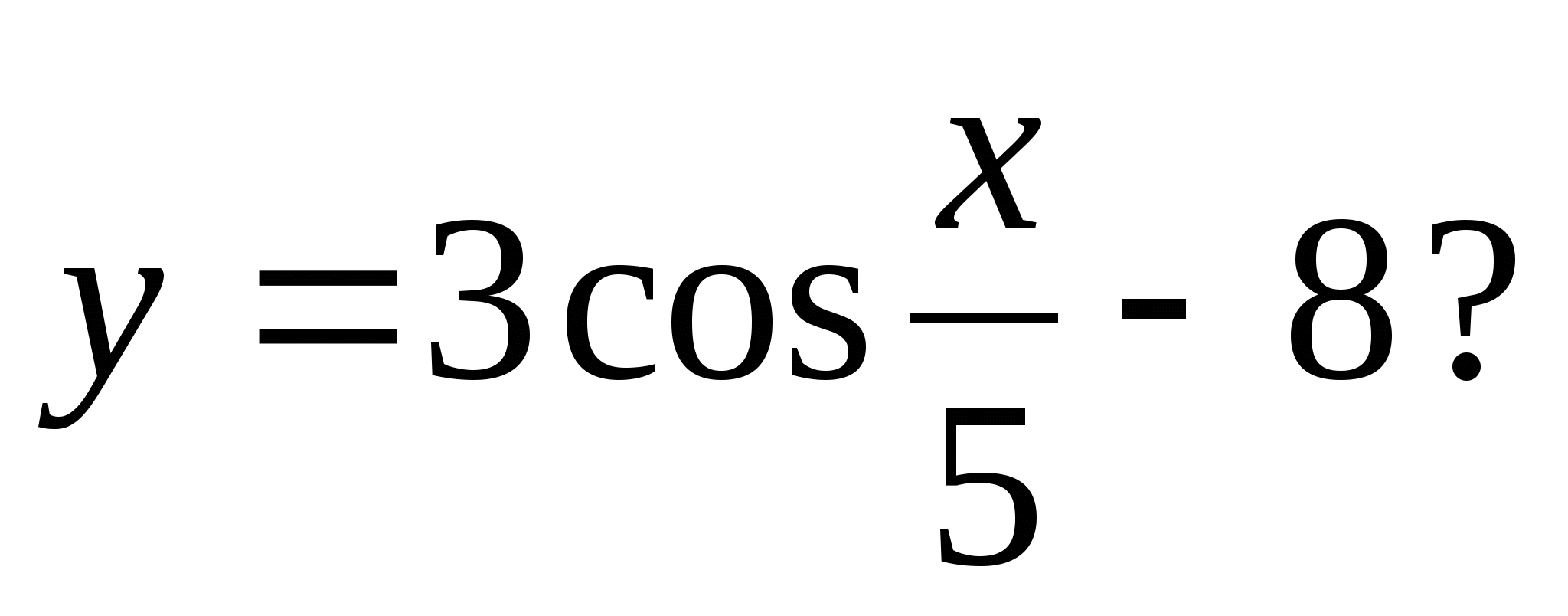

1) -6 2) -5 3) -10 4) -7

5. Укажите функцию, множеством значений которой является отрезок .

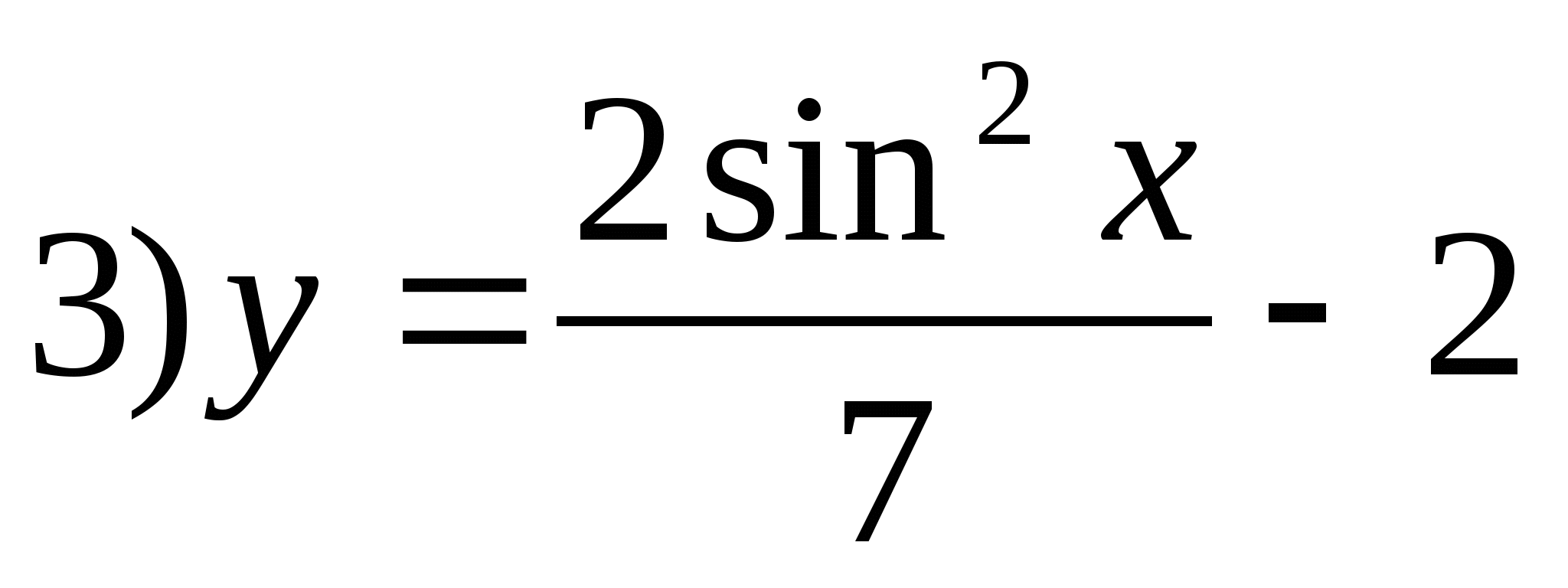
6. Укажите наибольшее целое отрицательное число, которое не входит в область значений функции

1) -1 2) -25 3) -6 4) -2

7. Сколько целых чисел принадлежит множеству значений функции

1) 11 2) 3 3) 5 4) 4

Вариант 5

1. Укажите множество значений функции у = 2 - sin 5 x .

1) (2;5) 2) 3) (1;3) 4) [-3;7]

2. Найдите область значений функции

1) [-8;-6] 2) [-8;-6) 3) (-8;-6) 4)

3. Укажите наименьшее целое число из области значений функции

y = 3 + sin 2 2 x .

1) 0 2) 1 3) 3 4) 4

4. Какое из следующих чисел входит в множество значений функции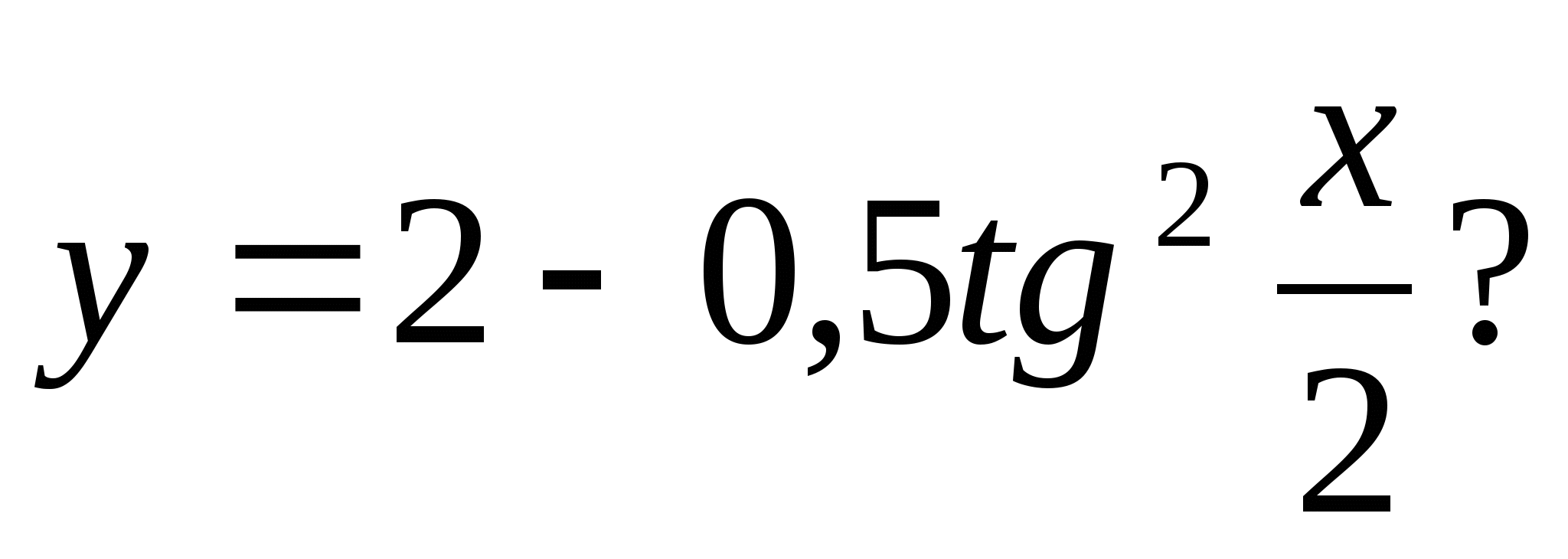

1) 128 2) 10,5 3) 3 4) -235

5. Укажите функцию, множеством значений которой является отрезок [-9;15].

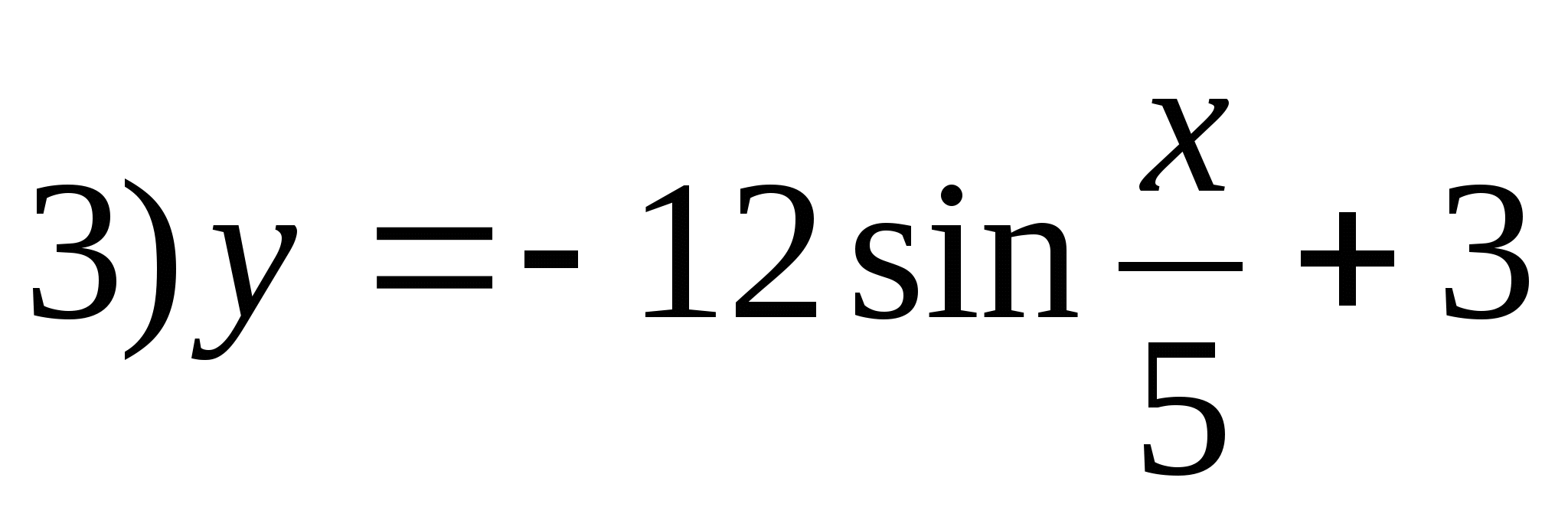
6. Найдите сумму целых чисел, входящих в множество значений функции

1) 0 2) 7 3) 18 4) 22

7. Найдите наибольшее значение функции
на отрезке

1) 0,5 2) 1,5 3) 0 4) 2

Вариант 6

1. Укажите отрезок, соответствующий множеству значений функции

1) 2) (-2;-1) 3) (0;1) 4) [-6;-4]

2. Найдите область значений функции

3. Укажите наибольшее число из области значений функции

1) 5 2) -6 3) -3 4) 4

4. Какое из следующих чисел входит в множество значений функции

1) 5 2) 0 3) -3 4) 4

5. Укажите функцию, множество значений которой является отрезок .

1) у = 15 – 7 cos 2x 3) y = 7 cos 2x + 3

2) y = 5 cos 4 x 4) y = - tg 2 x + 1

6. Найдите произведение целых чисел, входящих в множество значений

y = 3,8 – 1,4 sin 3 x .

1) 17 2) 12 3) 0 4) 60

7. Найдите множество значений функции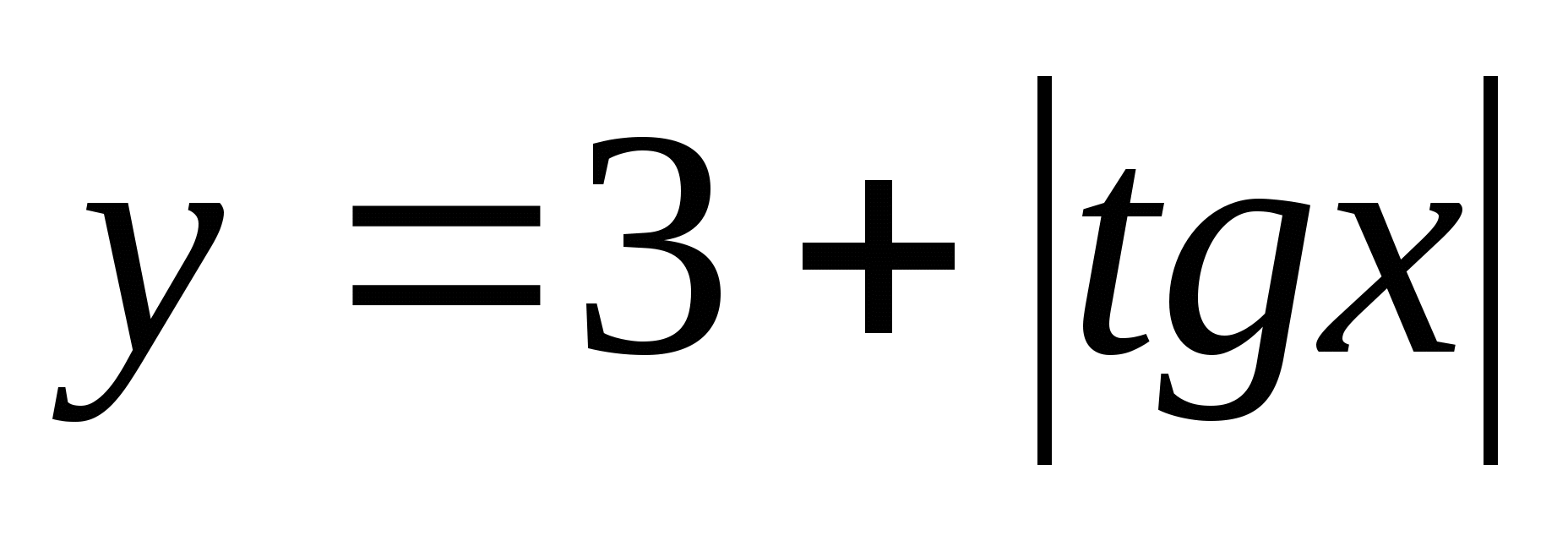
на промежутке

1) (3;4) 2) 3)

Вариант 7

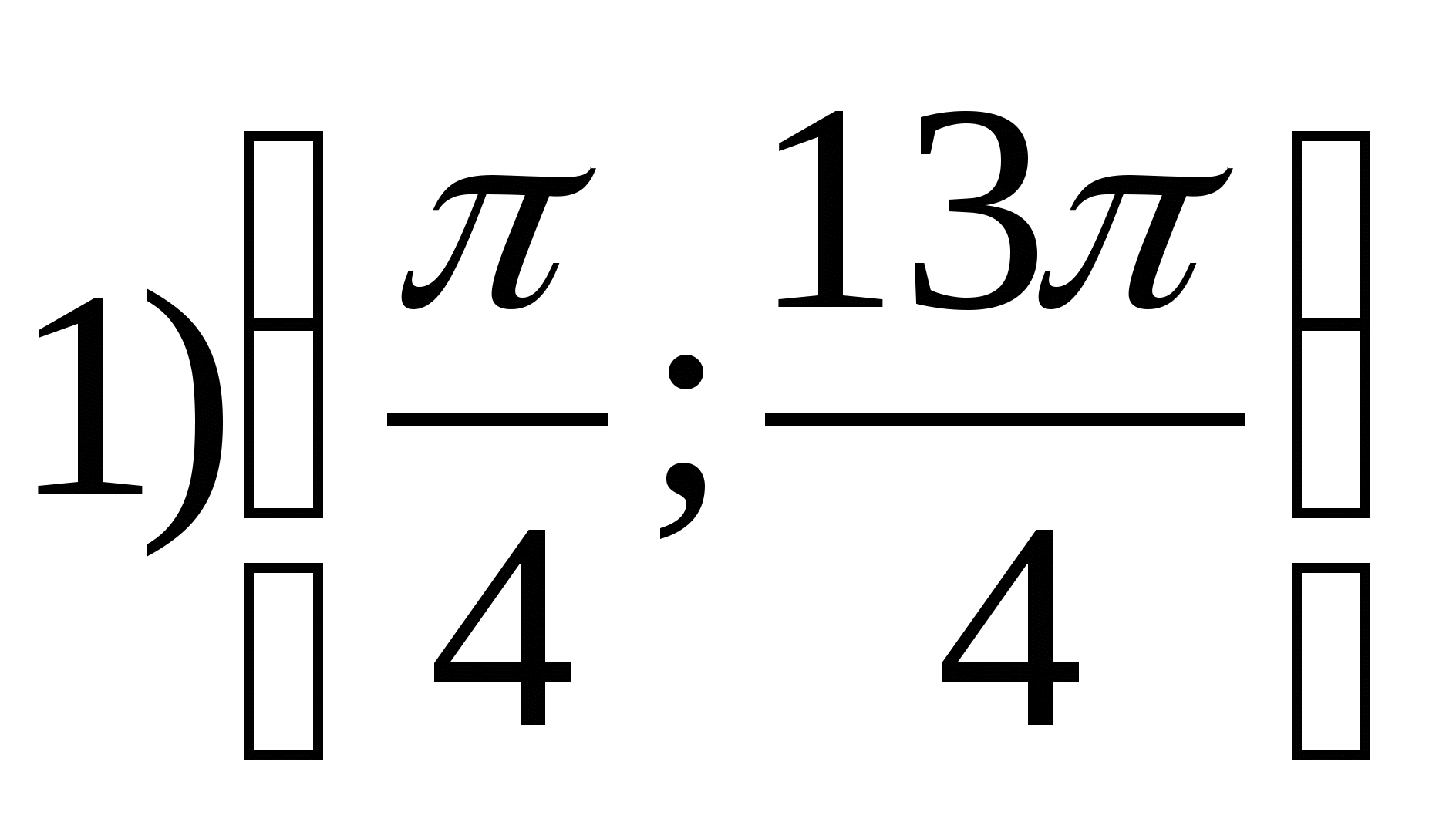
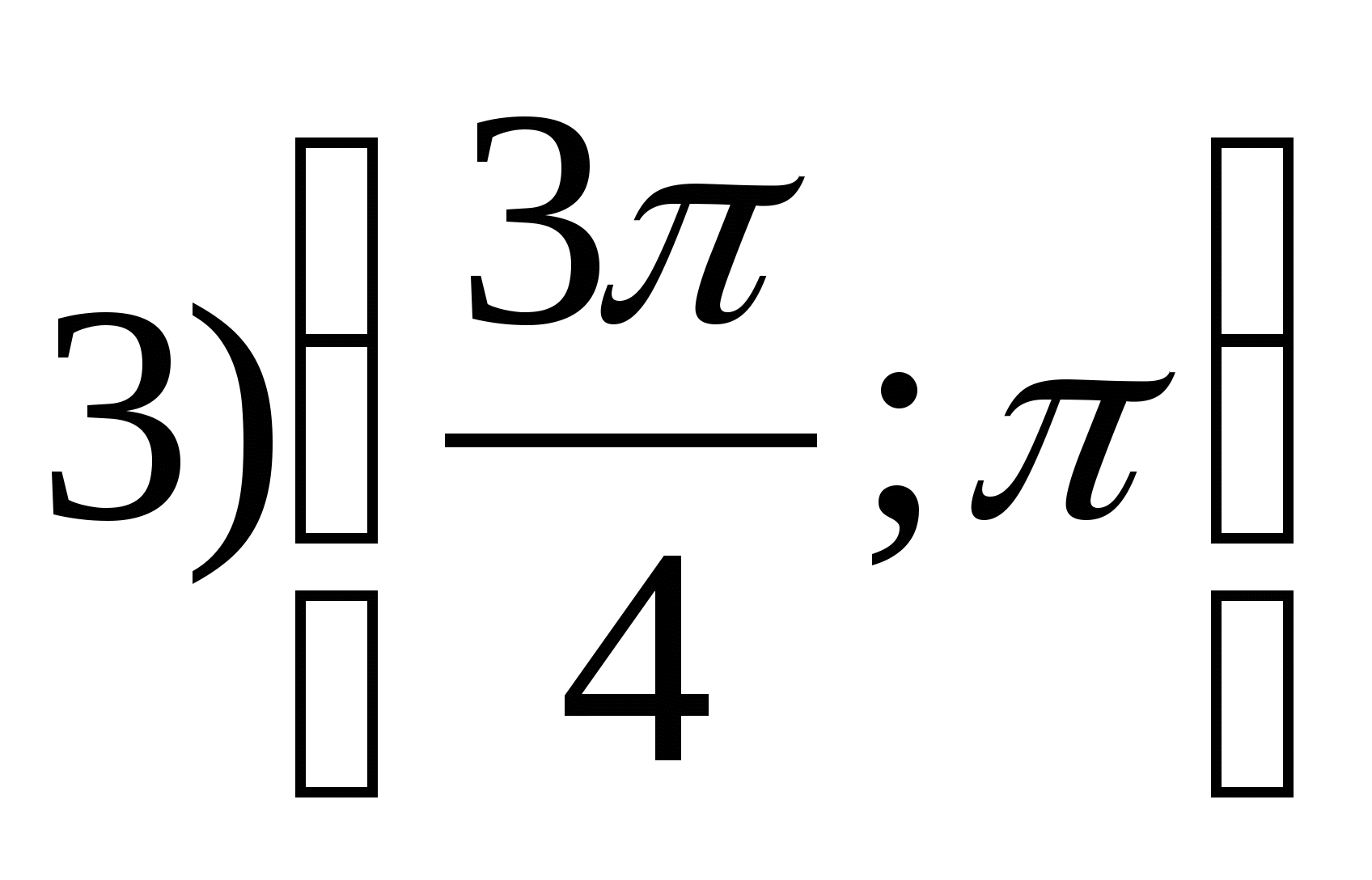
2. Найдите наименьшее целое значение функции

1) 2 2) 0 3) -3 4) -4

1) 0 2) 2 3) 4 4) 6

4. При каких значениях а уравнение sin (3 x -4)+5= a разрешимо?

1) 2) 3) (4;6) 4) (-6;4]

sin 2 2 x – 2.

1) [-3;-2] 2) [-1;0] 3) [-4;0] 4) [-3;-1]

на промежутке

2) 0 3) 1

y = 4 sin (x 4 ) -2?

1) 8 2) 9 3) 7 4) 10

Вариант 8

1. Найдите множество значений функции y = arctg x - 2π.

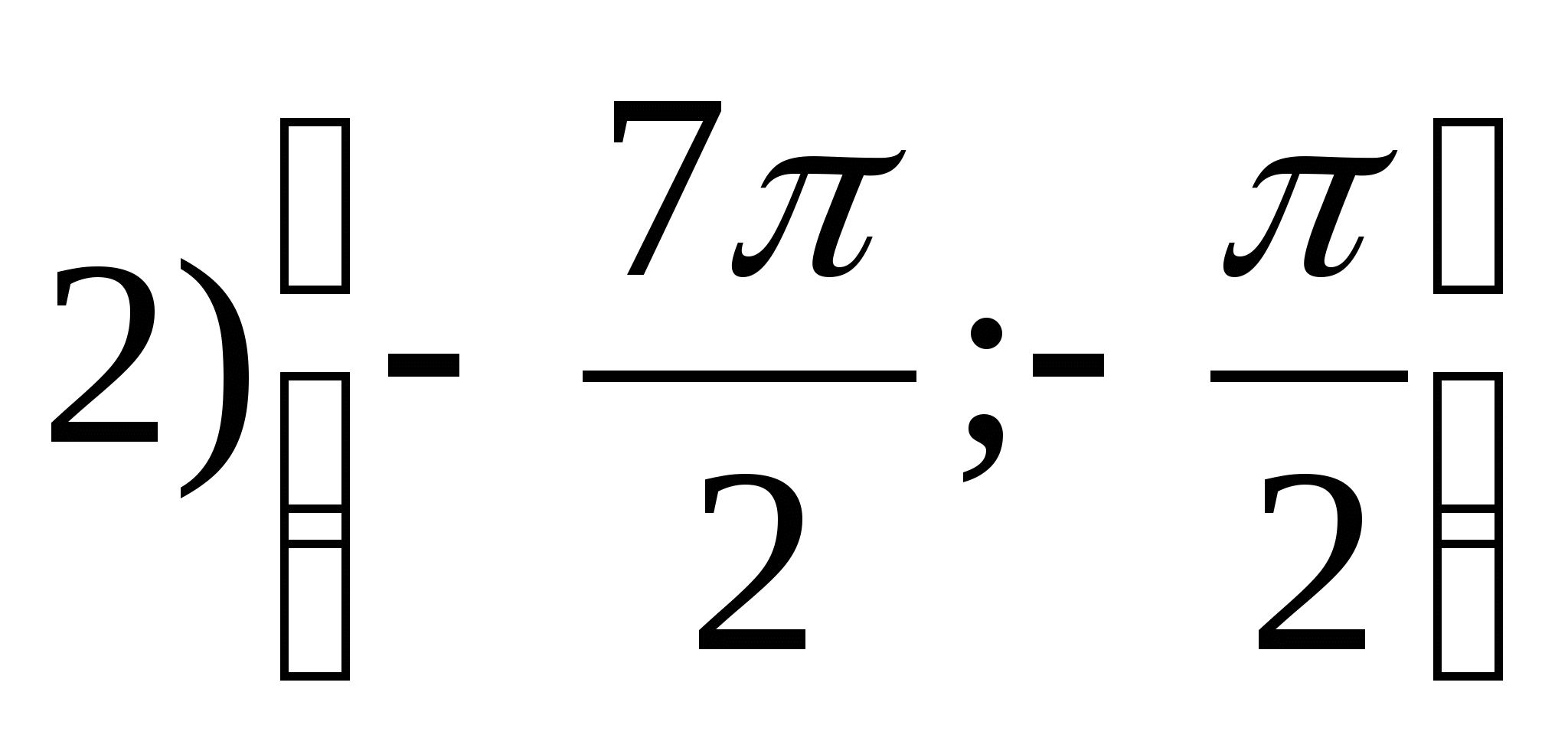
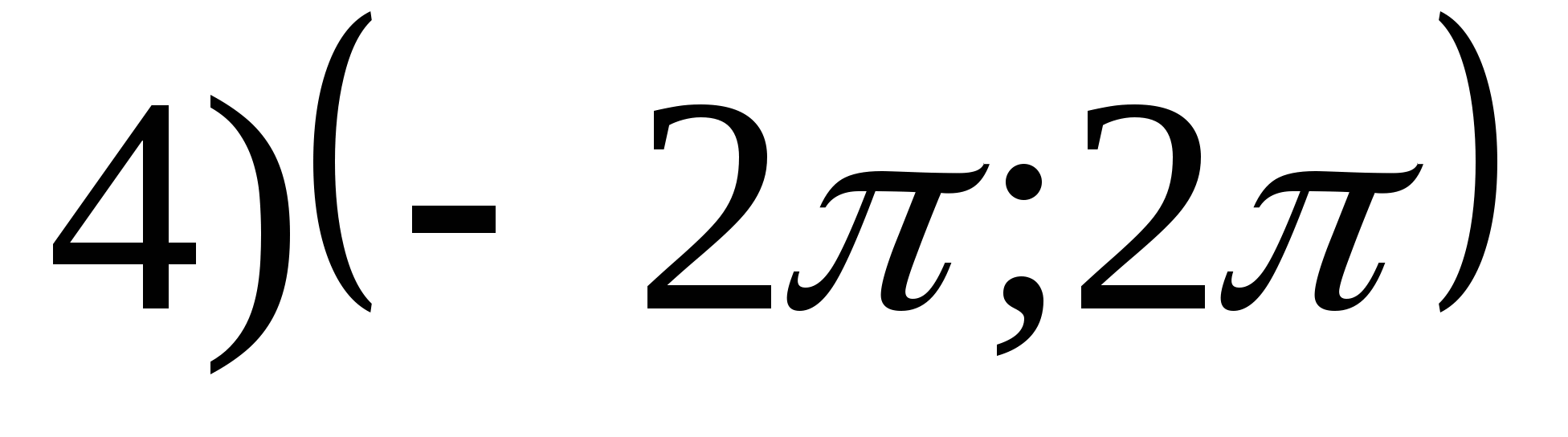
2. Найдите наибольшее значение функции

1) 1,75 2) 0 3) 2,25 4) -1,75

3. Какое из следующих чисел может быть значением функции

1) -4 2) -2 3) 0 4) 2

4. При каких значениях р уравнение -2+ cos (4 x -1)= p имеет корни?

1) [-3;-1] 2) [-3;-1) 3) (-3;1] 4) (-3;-1)

5. Найдите множество значений функции y = -2 tg 2 x + 1.

1) [-1;3] 2) (-∞;1] 3) (-∞;∞) 4) [-1;+∞)

на промежутке
.

1) 0 2) 1 3) -1 4) 3

7. Сколько целых чисел принадлежит области значений функции

1) 4 2) 3 3) 5 4) 2

Вариант 9

1. Найдите область значений функции

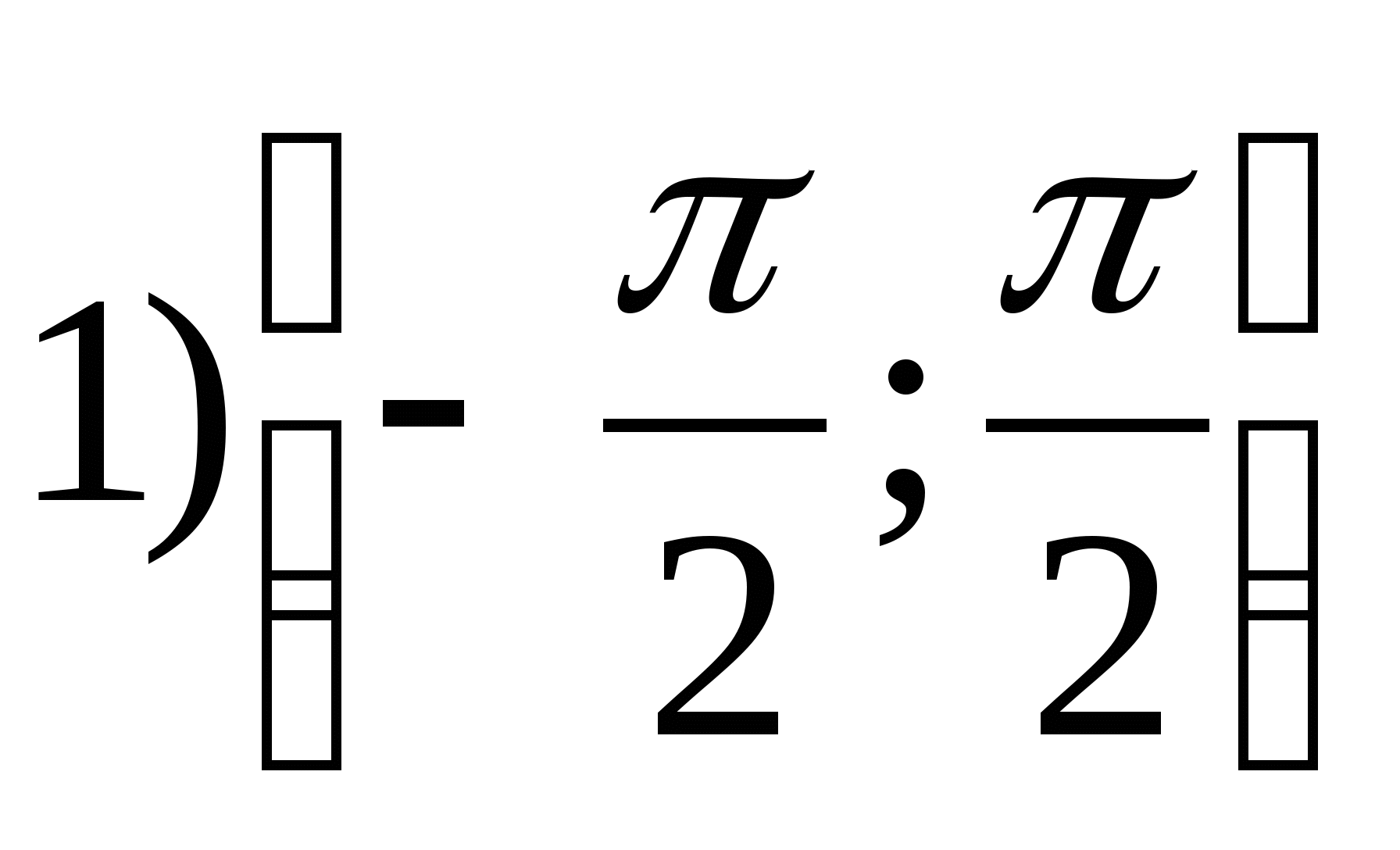
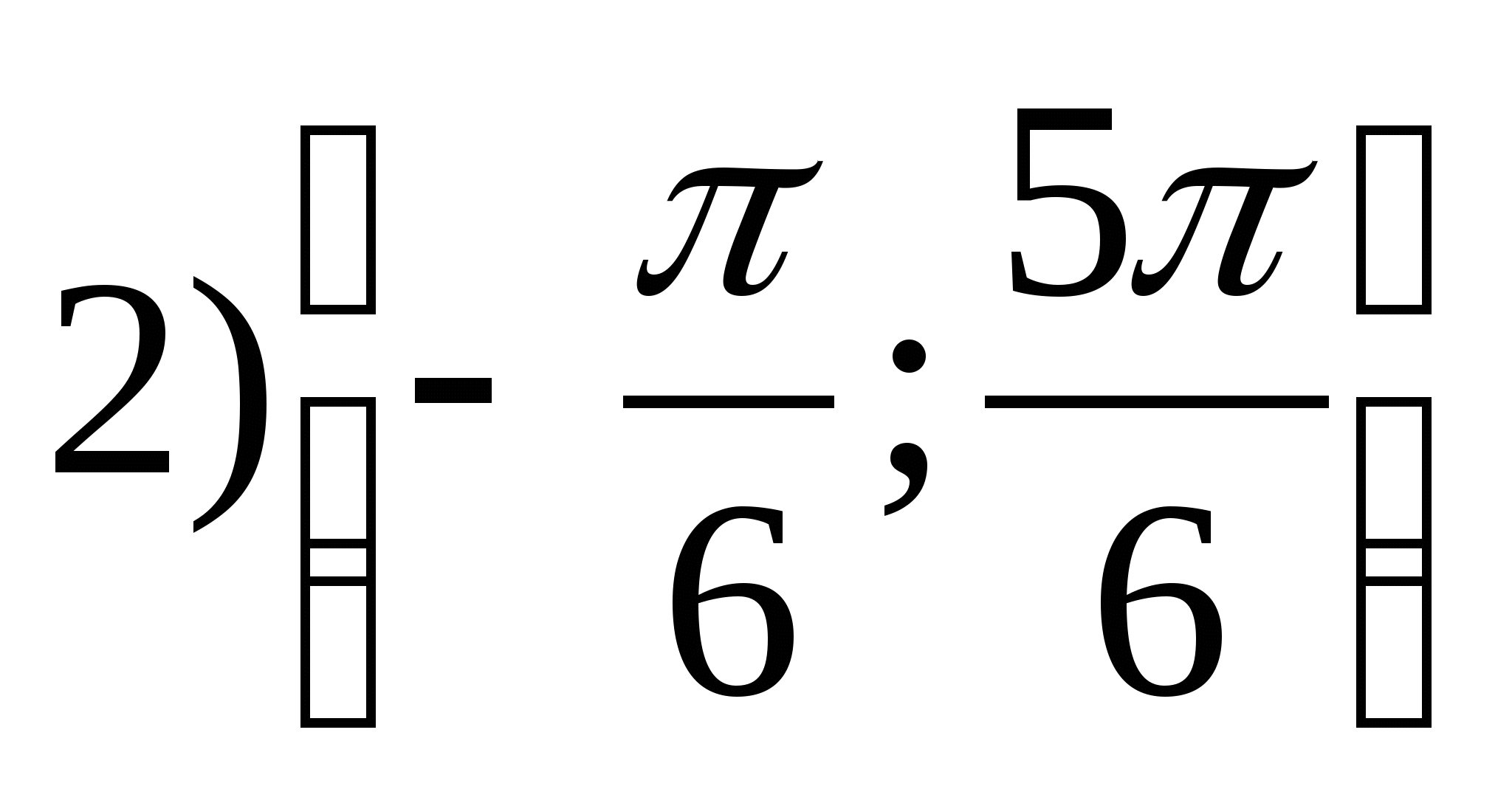
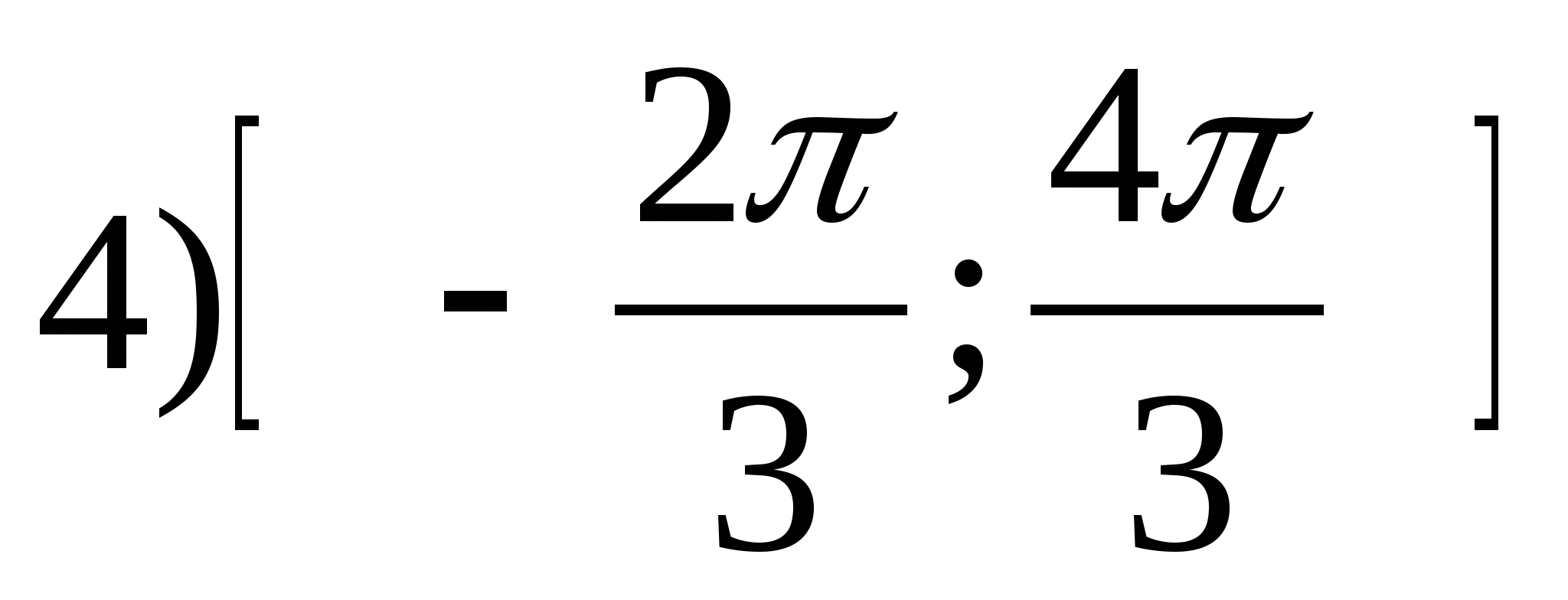
2. Найдите наибольшее целое значение функции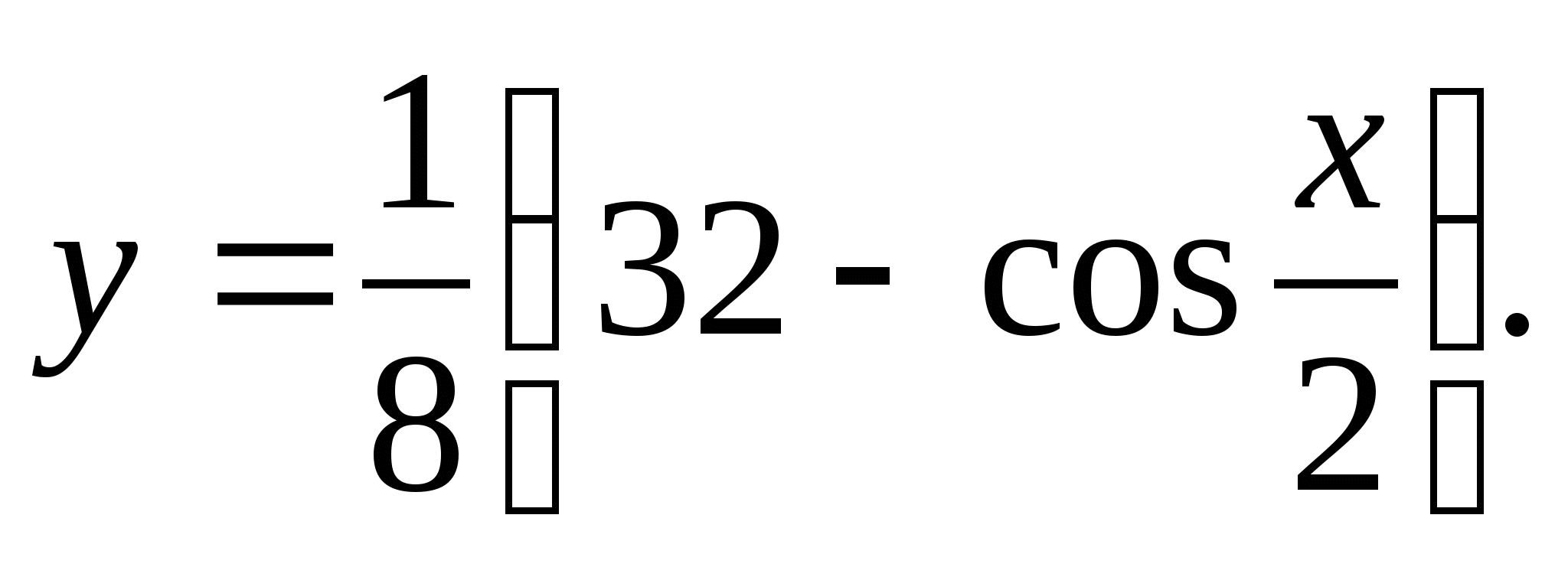

1) 4 2) 5 3) 6 4) 7

3. Какое из следующих чисел может быть значением функции

1) 0 2) 3 3) 6 4) 9

k уравнение – k + sin (2 x -1) = 2 разрешимо?

1) 2) (4;6) 3) (-3;-1) 4) [-3;-1]

5. Найдите множество значений функции у = - cos 2 3 x + 4.

1) 2) 3) 4)

6. Укажите наименьшее значение функции
на промежутке

2) -1 3) 0 4) 1

7. Найдите, сколько целых чисел входит в область значений функции у = 12 cos 3 x +5 sin 3 x .

1) 13 2) 27 3) 26 4) 14

Вариант 10

1. Найдите область значений функции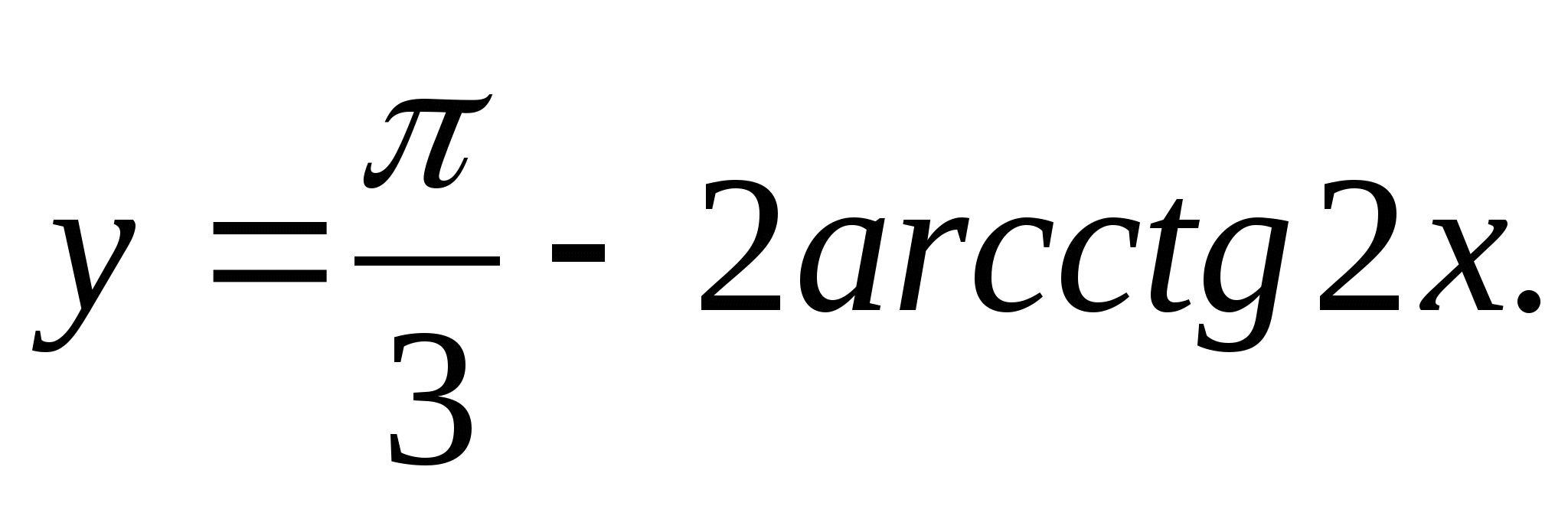

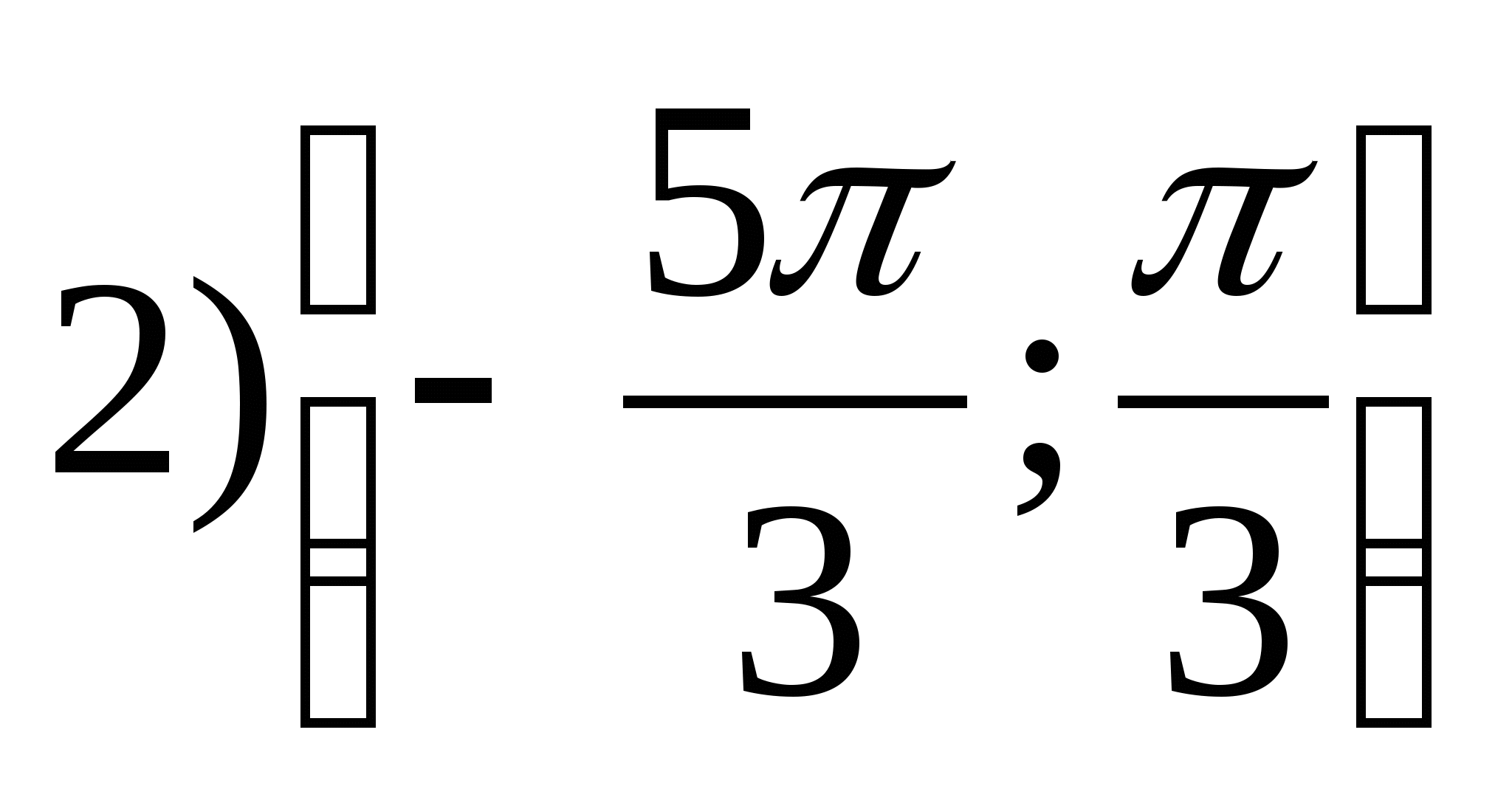
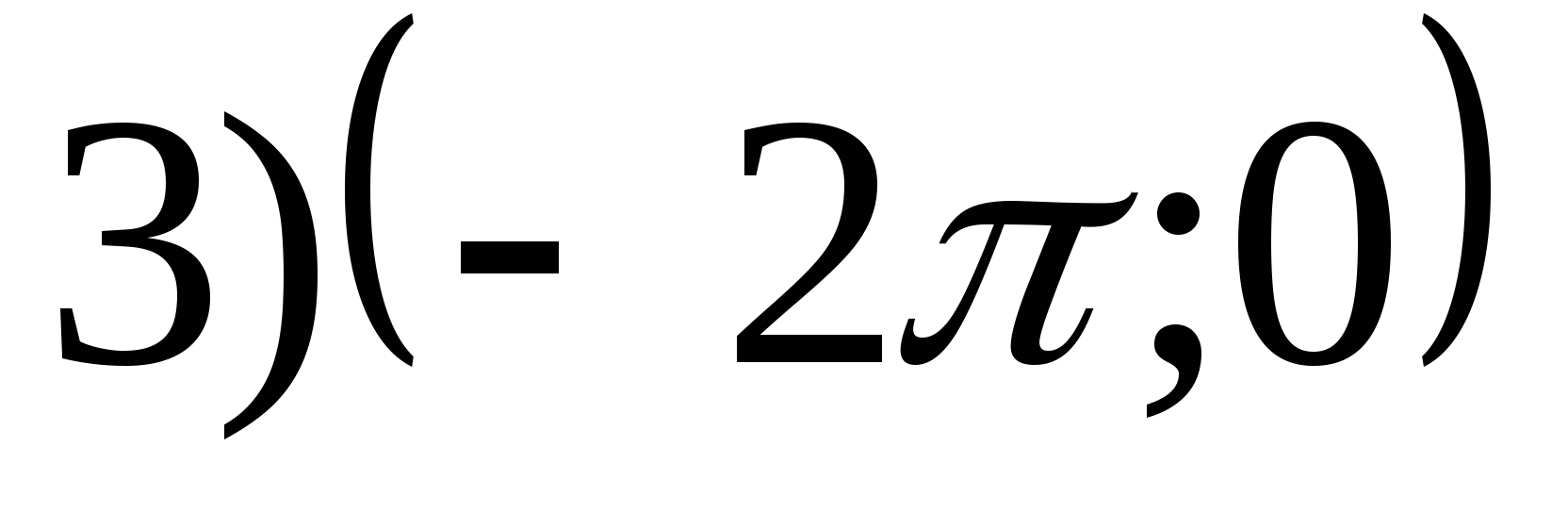
2. Найдите наименьшее значение функции

1) 3,5 2) 0 3) 2,5 4) -3,5

3. Какое из следующих чисел может быть значением функции

1) -4 2) -1 3) 3 4) 7

4. При каких значениях параметра m уравнение cos (3 x + 2)- m = 5 имеет корни?

1) [-6;-4] 2) (-6;-4) 3) (-4;3) 4) [-6;-5]

5. Найдите множество значений функции у = -2 ctg 2 3 x + 7.

1) (-∞;5] 2) (-∞;1] 3) (-∞;0] 4) (-∞;7]

6. Укажите наибольшее значение функции
на промежутке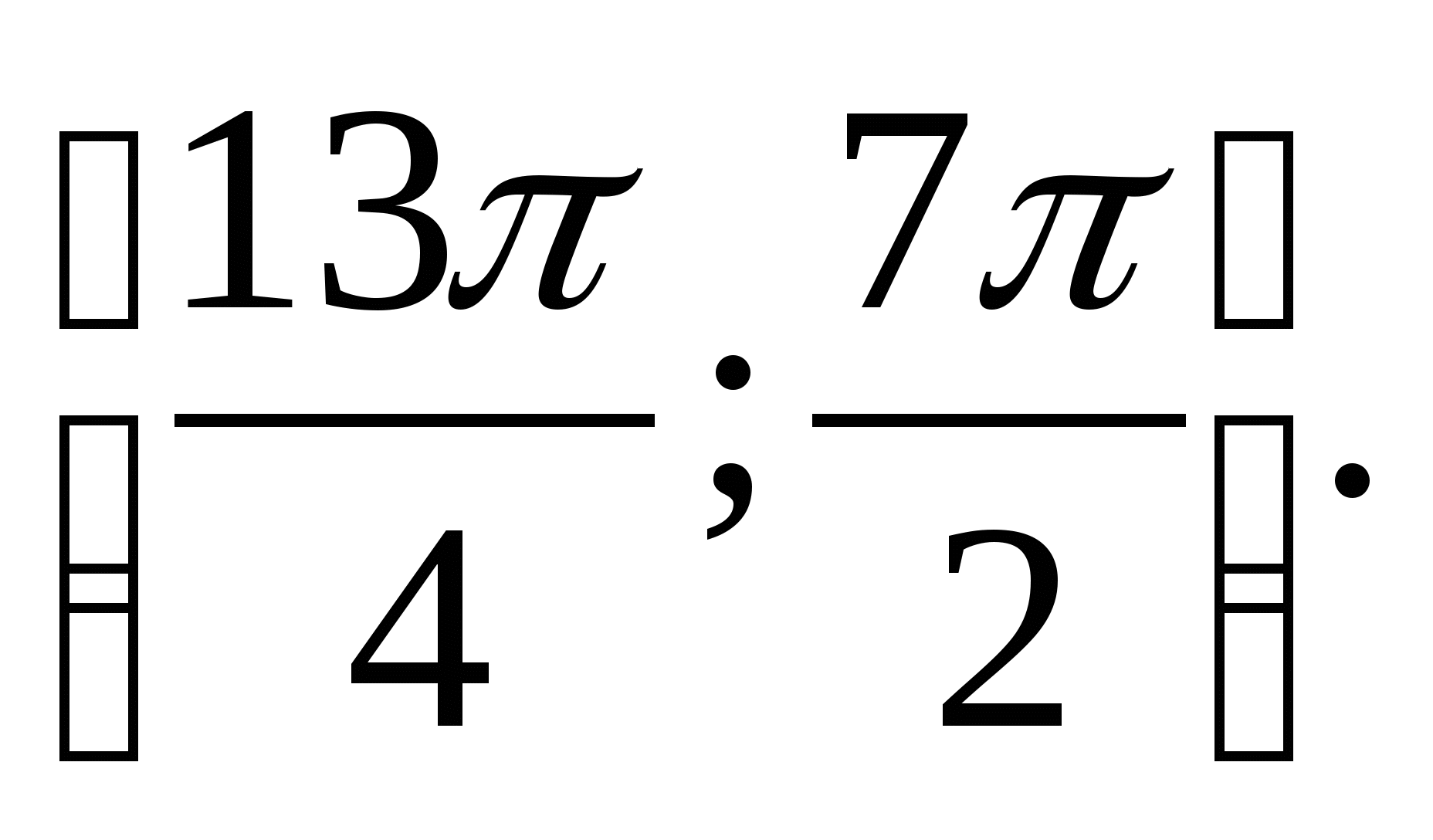

2) 0 3) 2 4) 1

7. Найдите, сколько целых чисел входит в область значений функции

1) 30 2) 35 3) 17 4) 7

Множество значений показательной и логарифмической функций

Вариант 1

1. Найдите область значений функции

1) 4) (-∞;3)

2. Укажите множество значений функции

1) (-∞;7) 2) (-∞;-7) 3)(7;∞) 4) (-∞;7]

1) 0 2) 4 3) -3 4) -4

1) 15 2) 20 3) 43 4) 28

1) (0;-2) 2) (0;2) 3) (-∞;+∞) 4) [-2;0)

6. Укажите наименьшее целое значение функции

1) 1 2) -1 3) 0 4) -5

7. Укажите функцию, множеством значений которой является промежуток (1;∞).

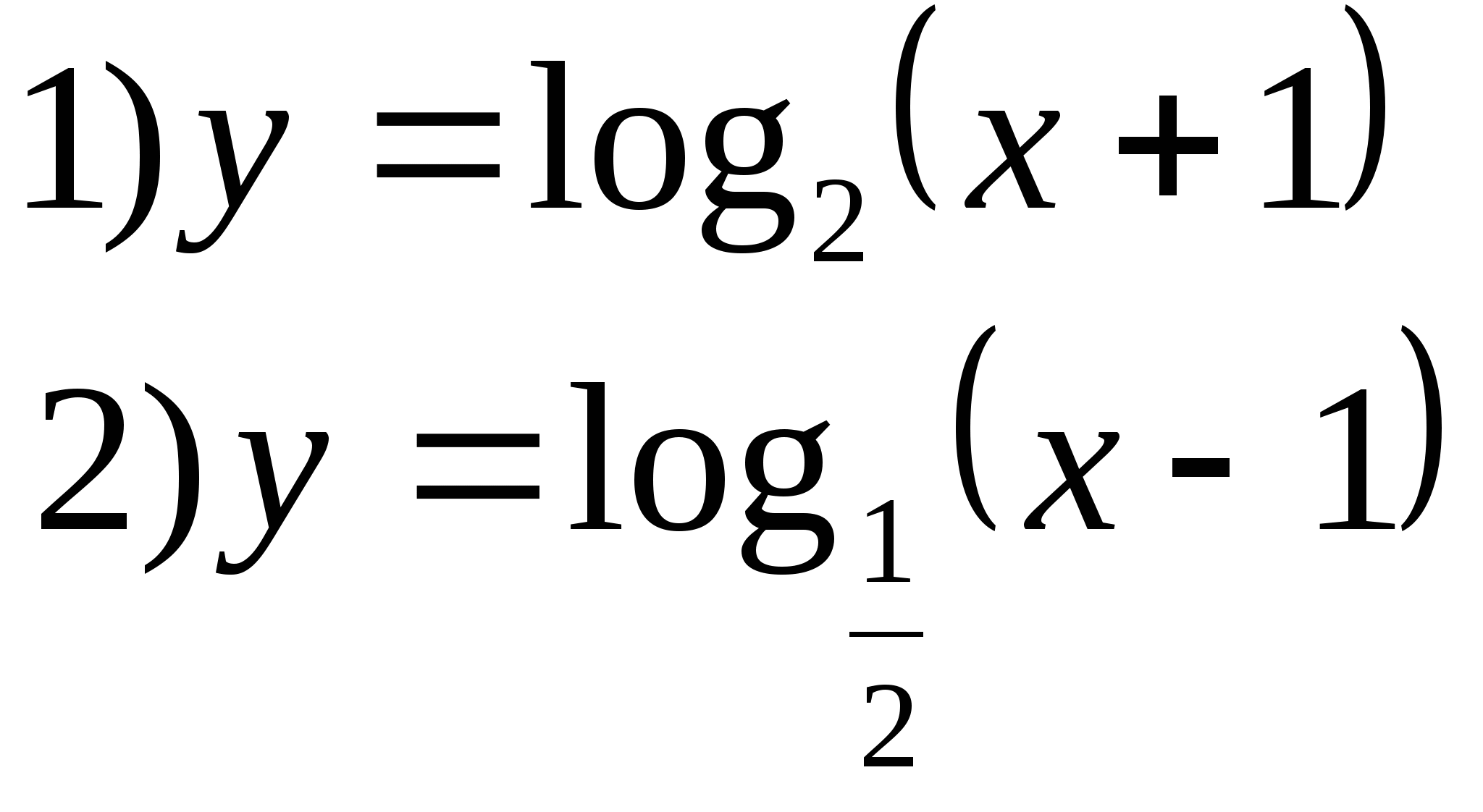
Вариант 2

1. Укажите множество значений функции

1) [-1;∞) 2)(-1;∞) 3) (3;∞) 4) 4) [-3;∞)

2. Найдите область значений функции

1) (-4;∞) 2) (4;∞) 3) (-∞;4] 4) 4) (-∞;4)

3. Укажите наименьшее целое значение функции

1) -12 2) -11 3) -10 4) -15

4. Укажите число, не принадлежащее множеству значений фунукции

1) -42 2) 3 3) 1 4) -20

5. Укажите множество значений функции

1) (-∞;0) 2) (0;∞) 3) (-∞;∞) 4) [-2;2]

6. Укажите наибольшее целое значение функции

1) 10 2) 3 3) 9 4) 2

7. Укажите функцию, множеством значений которой является промежуток

(-∞;13).

Вариант 5

1. Укажите наименьшее целое значение функции

1) 0 2) -1 3) -2 4) -3

2. Какое из следующих чисел входит в область значений функции

1) -3 2) -4 3) 5 4) 0

1) (-∞;2] 2) 2) [-1;1] 3) (-1;1) 4) (0;∞)

6. Найдите, на каком отрезке функция
принимает наибольшее значение, равное 2, и наименьшее значение, равное -3.

1) 2) (-5;2) 3) 4) (-3;2)

на промежутке

1) -1/2 2) 5 3) 2 4) 4

8. Найдите сумму всех натуральных чисел, не входящих в множеств значений функции

1) 3 2) 6 3) 10 4) 8

Вариант 6

1. Укажите наибольшее целое значение функции

1) 2 2) 4 3) 3 4) 5

2. Какое из следующих чисел не входит в область значений функции

1) 35 2) 7, 28 3) 7, 85 4) 128

3. Укажите множество значений функции

1) [-1/3;0] 2) (-3;2/5) 3) (0;1/3) 4) (0;2/5)

4. Найдите все точки на ОУ, являющиеся проекциями точек графика функции

1) (0;∞) 2) 2) (-3;2) 3) [ log 2 3;2] 4) (log 2 3;2)

6. Найдите на каком отрезке функция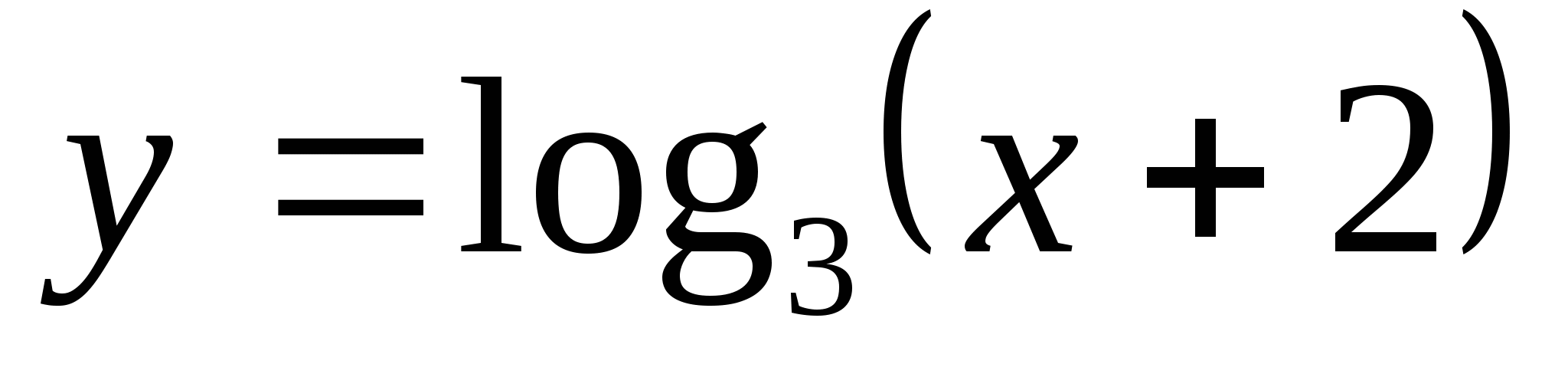
принимает наименьшее значение, равное -2, и наибольшее значение, равное 4.

1) [-17/9;79] 2) [-1,5;82] 3) (-11/9;79] 4) (-17/9;79)

7. Укажите наибольшее значение функции
на промежутке

[-0,9; 0]. 2. Найдите наименьшее значение функции на отрезке .

4. Сколько целых значений принимает функция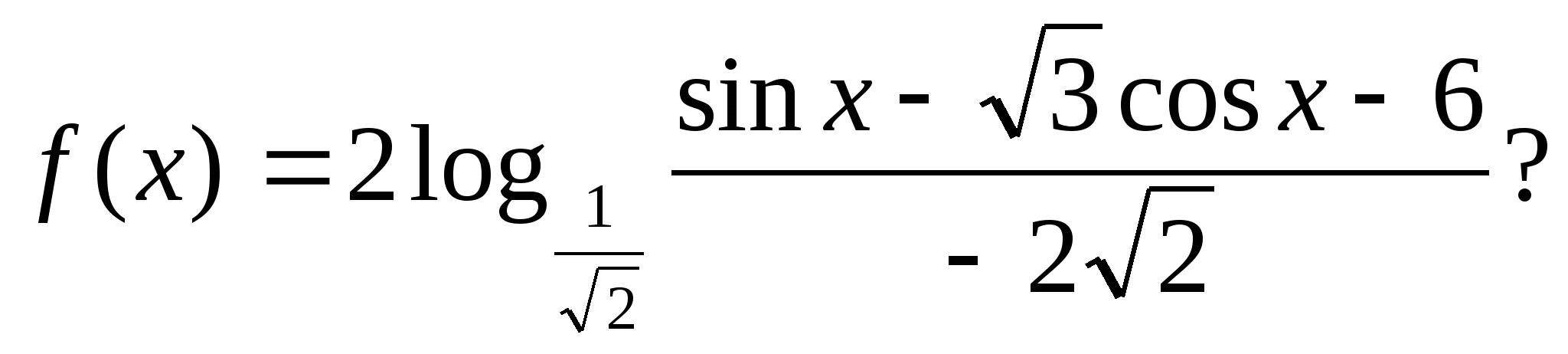

Ответы

Часть 1

Множество значений показательной и логарифмической функции

Часть 2